理科専科は、授業開きってどうするの？！　〜５生編〜

理科専科が授業開きで大事にしていることとは？

　前回は、理科専科が授業開きで何を大事にしているのかについて説明しました。まだ読まれていない方は、先に　「理科専科はどう考える？！　〜理科の授業開き〜」をご覧ください。

　しかしながら、読まれた方の中には、「それって具体的にはどんな授業なの？」って思われた方もいるかと思います。そのため、今回は、理科専科は５年生の授業開きをどうしているのかについて紹介したいと思います。

５年でつけたい問題解決能力は？

　まず、５年生で身につけたい問題解決能力を確認しましょう。学習指導要領では…

　第５学年では，主に予想や仮説を基に，解決の方法を発想するといった問題解決の力の育成を目指している。この力を育成するために は，自然の事物・現象に影響を与えると考える要因を予想し，どの要因が影響を与えるかを調べる際に，これらの条件を制御するといった考え方を用いることが 大切である

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　【理科編】小学校学習指導要領（平成29年告示）解説

と明記されています。これは、どういうことかというと…

　例えば、「電磁石の強さをつよくするにはどうすればいいのか？」という問題に対して、子どもたちは色々な予想を立てます。

などです。しかしながら、これらの予想の中でどれが真実なのかを子どもたちはわかっていません。そこで、実験をして確かめるのです。

　たとえば、「導線の太さを太くする」という予想が正しいのかどうかを確かめるために、「①導線の太さを５mm、電流の強さは電池１個分、巻数は１００回巻き　と　②導線の太さを１mm、電流の強さは電池１個分、巻数は２００回巻き」を比べるという実験をしたとします。しかしながら、この実験は、ブーです。なぜかというと、電磁石が強くなったとしても、それが「導線の太さ」によるものなのか「巻数」によるものなのかがわからないからです。つまり、仮説（怪しいと思う条件）を立てた後は、その条件だけを変えて、他の条件は同じにする必要があるのです。そのため、正しい実験方法は「①導線の太さを５mm、電流の強さは電池１個分、巻数は１００回巻き　と　②導線の太さを１mm、電流の強さは電池１個分、巻数は１００回巻き」を比べるというものになります。こんな風に条件制御をしながら、子どもたちが実験方法を発想できるような力をつけていくのが５年生ということになります。

東京書籍は、５年生の授業開きをどうしているのか？

　では、東京書籍では５年生の授業開きをどうしているのでしょうか？

　東京書籍の１ページを開いてみると、生卵とゆで卵の写真が大量にはってあり、「どこまでがなまたまご？どこからがゆでたまご？」という問題が出されています。みなさんは、この授業開きをどう思いますか？

　私は、「うーん」と思います。理由は、「問題解決ができないから」です。理科って問題解決が楽しい教科なのに、１発目に問題解決をさせないのは、自分の中ではありえません。しかも、これの答えってすごく曖昧だと思うんです。生卵とゆで卵の境って自分もわかりません。それを子どもに求めるのって「どうなのかな？」って思います。じゃあ、自分はどんな授業開きをしたのか紹介します。

板書案

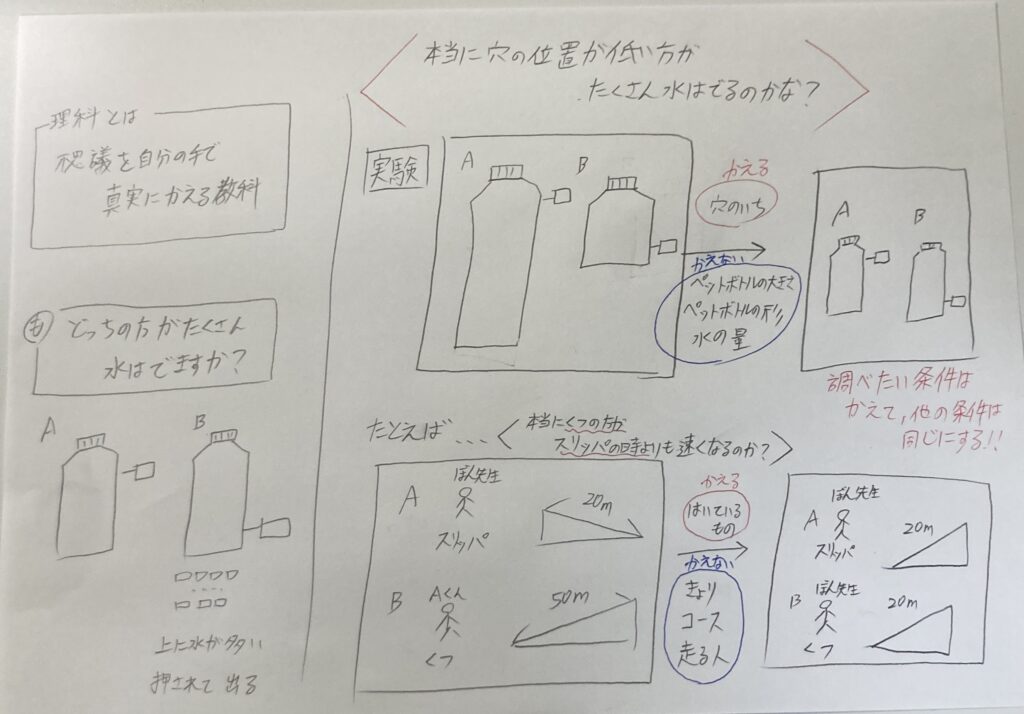
理科とはどんな教科なのかを確認する

T：今日から皆さんと理科の授業をします。ぼん先生です。よろしくお願いします。

C：よろしくお願いします

T：そしたら、さっそくなんだけど、みなさんに質問があります

C：はい

T：理科ってどんな教科ですか？

C：うーん

T：ペアで相談

C：できました

T：おしえて

C：はい

T：Aさん

C：はい。実験する教科です

C：ほかにあります

T：Bさん

C：外に出て生き物を見たり、植物を育てたりする教科だと思います

C：他にあります

T：Cさん

C：ふしぎを解決する教科だとおもいます

C：わかりました

T：なるほどね。そしたら、ぼん先生は、理科ってこんな教科だと思っているよっていうのを書くね。みんなもノートにかいてね。

C：はい

C：できました

T：先生は、これが理科だと思っているの。

C：あ〜

T：理科では、生き物みつけたり、植物育てたり、実験したりするんけど、それが目的というわけではないよ。だから、実験して「あ〜たのしかった」ではだめだよってことね。

T：自分で不思議見つけて、自分なりの予想を立てて、それが本当にあってるか確認するために実験や観察をして、ほんで自分なりの答えをだす。これが理科だよ。わかった？

C：はい

T：そしたら、今日は１回目ということで、「不思議を自分の手で真実に変える」っていうのを実際に体験してみようね

問題をつかみ、予想させる

T：そしたら、今日はこんなのを持ってきました。じゃーん

C：ペットボトル

T：中には何が入っているかというと

C：水です

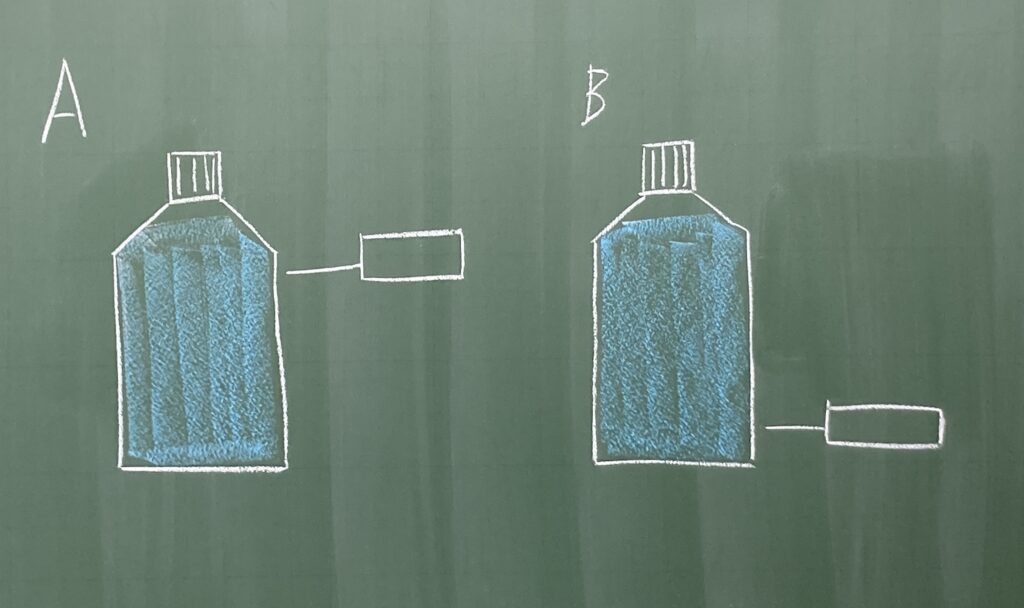
T：今回は、それを２本準備して、Aはこのへんにキリをさします。ほんでBはこのへんにキリをさしまう。２つを比べるとどこがちがう？

C：はい

T：Eさん

C：穴の位置です

T：そうだね。じゃあ、問題ね

C：え〜

T：じゃあ、１回自分の席に戻って、ノートに問題書いて

C：できました

T：そしたら、選択肢は何がある？

C：A

C：B

T：あともう一つあるよ

C：変わらない

T：そうだね。じゃあ、自分の考えと理由をノートにかいてみてください。どうぞ

C：はい

C：できました

T：じゃあ、正しいと思うところにネームプレートをはりにきてください

C：はい

T：お〜

C：全員Bだ

T：え〜何でそう思ったの？

C：はい

T：Fさん

C：はい。穴より上の水が出ると思うので、穴のいちが低いBを選びました

C：おなじです

C：つけたしです

T：Gさん

C：はい。上の水に押されて、穴から水がたくさんでると思ったから、Bをえらびました

C：わかりました

T：なるほどね。でも、それって本当にただしいのかな？

C：わかりません

T：じゃあ、今日の課題はどうする？

C：本当に穴の位置が低いほうがたくさん水は出るのかな？

T：じゃあ、それでいこう

ということで、本時の課題として『本当に穴の位置が低いほうがたくさん水はでるのかな？』と決まりました。ちなみに、この課題の立て方は、すごく便利なので詳しく知りたい方は、「理科専科はどう考える？！　〜理科の課題づくり〜」を読んでみてください。

【重要】　実験方法のどこがちがうのかな？

T：じゃあ、今から実験をしようね。

C：はい

T：ということで、今回は、ぼん先生が先にペットボトルとかの準備をして持ってきたよ。じゃーん

C：？

T：あれ？どうしたの？

C：先生。これっていいんですか？

T：どういうこと？もう少し詳しくおしえて

C：なんか、２つのペットボトルがぜんぜん違います

T：なるほどね。でも、２つのペットボトルがちがってたらだめなの？

C：うーん

T：じゃあ、説明はできないけど、なんか駄目な感じがするってこと？

C：はい

T：なるほどね。実は、その感覚は正しいよ。このまま実験してもAとBでは条件がいろいろちがうからだめなの

T：じゃあ、たとえばなんだけど⋯みんなってスリッパで走るのと、靴で走るのだったら、どっちが速いとおもう？

C：くつ

T：へ〜。でもそれって本当に正しいの？

C：たぶん

T：ということで、「本当に靴のほうがスリッパのときよりも早くなるのか？」っていうふうに課題をたてたとしよう

C：はい

T：ほんで、今からこんな実験して、こんな結果が出たとしよう

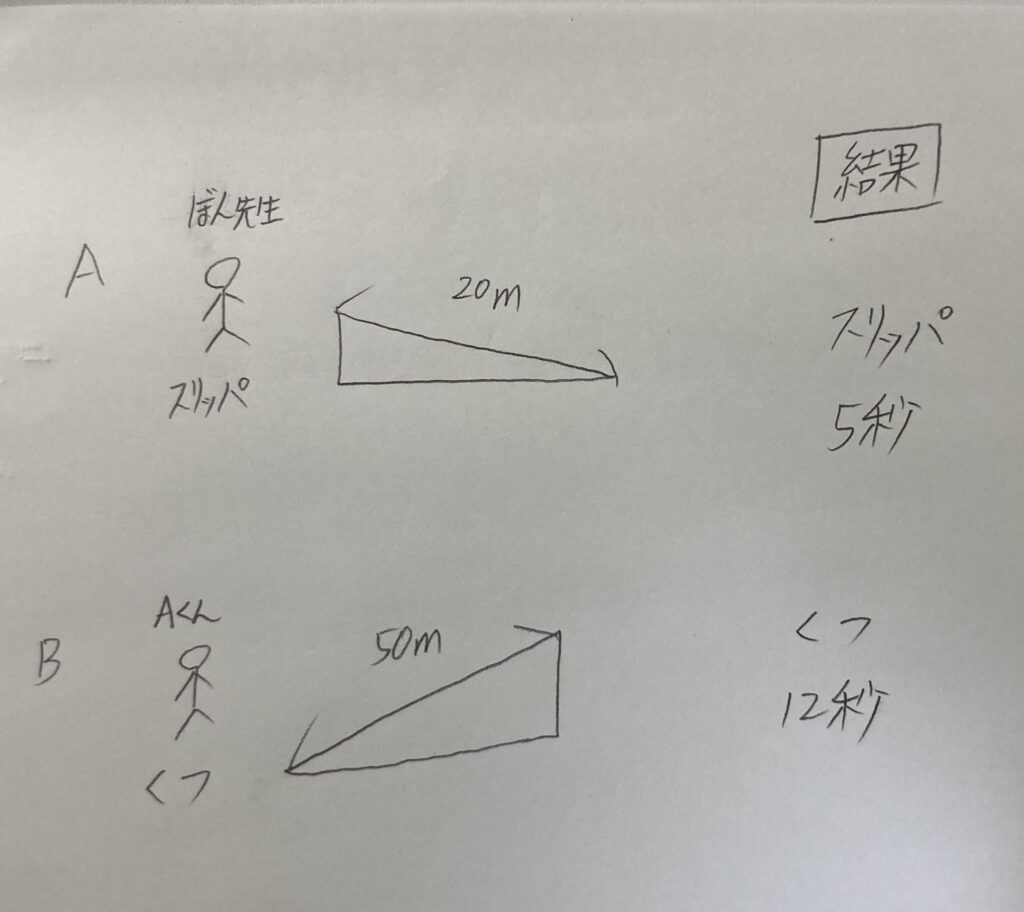
T：スリッパは５秒、くつは１０秒。このことからスリッパのほうが速い

C：え〜

T：納得じゃないの？

C：はい

T：なんで？

C：だって、Aは距離が短いけど、Bは距離が長いから

C：だって、Aは下り坂なのに、Bは上り坂だから

C：だって、Aはぼん先生が走っていて、BはAくんが走っているから

T：そうだよね。今回、このタイムには、「距離」「コース」「走る人」「履いているもの」といったいろいろな条件が関係しているわけだよね。その条件がバラバラだったら、納得できる？

C：できません

T：だよね。そしたらAとBで条件をそろえないといけないね

T：Aの距離は、２０ｍ。じゃあ、Bは？

C：２０ｍ

T：Bのコースは、上り坂。じゃあ、Bは？

C：上り坂

T：Aの走る人はぼん先生。じゃあ、Bは？

C：ぼん先生

T：Aはスリッパ。じゃあ、Bは？

C：スリッパ

C：いや、靴

T：意見バラけたよ？

C：絶対靴だよ。だって、今、靴とスリッパでどっちが速いかを比べたいから、これは変えないとだめじゃん

C：たしかに

T：その通り。だから、Bは靴だね。

T：こんなふうに、理科では、仮説を立てたら、調べたい条件は変えて、他の条件は同じにして実験しないとだめだよってことね。

T：このとき２つ条件が変わったら、どっちが原因かわからなくなるの。例えば、履いているものも変えて、コースも変えたとするよ。このとき、「履いているもの」が違うから、タイムに影響が出たのか、コースが違うからタイムに影響が出たのか区別つく？

C：つきません

T：だよね。だから、調べたい条件は変えて、他の条件は同じにするっていうのが大事なの

T：じゃあ、戻って。これで実験したらどう？

C：だめ。

T：そうだよね。全然条件揃ってないよね。比べてみて、どこが違う？

C：Aのほうが穴の位置が高いです

C：Aのほうがペットボトルがおおきいです

C：Aのほうがペットボトルの形がすらっとしてます

C：Aのほうが水がたくさん入っています

T：すごい。そしたら、Aがたくさん水が出たとしても、それは、「穴の位置」のおかげなのか、「ペットボトルの大きさ」のおかげなのか、「ペットボトルの形」のおかげなのか、「水の量」のおかげなのかわからないよね。だから、条件を揃えてあげないといけないってことだね。

C：なるほど

T：じゃあ、実際に準備するよ。このペットボトルをつかうの。もう１本はどのペットボトルをつかえばいい？

C：一番右です

T：そうだね。これで、「ペットボトルの大きさ」と「ペットボトルの形」が揃うね。じゃあ、水をいれてきましょう。きょうりょくしてね

C：はい

C：できました

T：どうけ？

C：一緒です

T：穴はどこにさせばいい？

C：Aはこのへんで、Bはこの辺です

T：そうだね。

T：今回、課題が「本当に穴の位置が低いほうがたくさん水はでるのかな？」だから、変える条件は何かっていうと？

C：穴の位置

T：ですね。ほんで、他の条件は同じにしないとだめで、今回で言えば他の条件ってなんのこと？

C：ペットボトルの大きさ

C：ペットボトルの形

C：水の量

T：ということだね

T：ほんで、今は予想はBなんだよね。じゃあ、どんな結果になればいい？

C：Bがたくさん水が出ればいいです

条件制御しながら実験し、ふりかえりをする

T：ということだね。じゃあさすね。よし抜くよ。えいや

C：！

C：水がでない

T：ということで、これ真実は、変わらないなんですよ

C：え〜なんで？

T：なにがなんでなの？

C：なんで水が出てこないのかなって思いました

T：なるほどね。なんでやと思う？

C：うーん

T：他のクラスでは、もしかしたら穴の大きさが小さすぎるからじゃないかなって言ってたわ

C：たしかに。穴の大きさが変わったらどうなるんやろう？

T：気になるね。でも、今回はここまで〜

C：え〜

T：時間がきたもん。ごめんね笑

T：こんなふうに、５年生では、実験方法を発想する力を鍛えます。コツは、「調べたい条件は変えて、他の条件は同じにする」です。５年生の最後には、自分で実験方法を立てられるようになろうね

C：はい

T：じゃあ、ふりかえりをしてね

C：はい

C：できました

T：実験方法を立てるときに大事なことは何？

C：調べたい条件だけ変えて、他の条件は同じにする

T：ですね

おわりに

　どうでしたか？子どもたち、すごく楽しそうじゃないですか？じゃあ、何故楽しそうなのかと言うと、問題解決を子どもたちにさせたからだと思います。こうすれば、子どもたちは、「理科楽しそう」って思うんだろうし、「どんどんやりたい！」ってなると思います。

　また、「理科専科は、授業開きってどうするの？！　〜４年生編〜」を見られた方は感じたかもしれませんが、素材はほとんど同じなんです。実は、これ！あえてなんです！！！授業開きに力を入れたいけど、４月はどうしてもバタバタするじゃないですか？これだと、見せ方を変えただけで、準備はほとんど要りません。でも、それぞれの学年でつけたい問題解決能力を意識させることはできると思います。ぜひ、試してみてはいかがでしょうか？

　もし、４年生でペットボトルにきりを指す実験を見せているのなら、①ペットボトルにきりを指しても水をでないことを確認する。②「ふたをあけたら、AとBはどっちがたくさん水がでるか」について予想させるっていうふうに、「ふたをあける」っていうのをいれると良いと思います。

　他の授業開きシリーズについて気になる方は、「理科専科はどう考える？！　〜理科の授業開き〜」「理科専科は、授業開きってどうするの？！　〜６年生編〜」「理科専科は、授業開きってどうするの？！　〜４生編〜」「理科専科は、授業開きってどうするの？！　〜３生編〜」を御覧ください。

　また、ぼん先生がこのブログを通して実現したいことをまとめました。気になる方は、ぼん先生のやりたいこと　〜自己紹介〜をご覧ください。