理科専科がズバリ授業案を公開！　〜４年「電流のはたらき」２授業目〜

　まだ１授業目を見ていない方は先に理科専科がズバリ授業案を公開！　〜４年「電流のはたらき」１授業目〜を御覧ください

＜乾電池の向きが反対になると、モーターの回る向きが反対になるのはどうして？＞

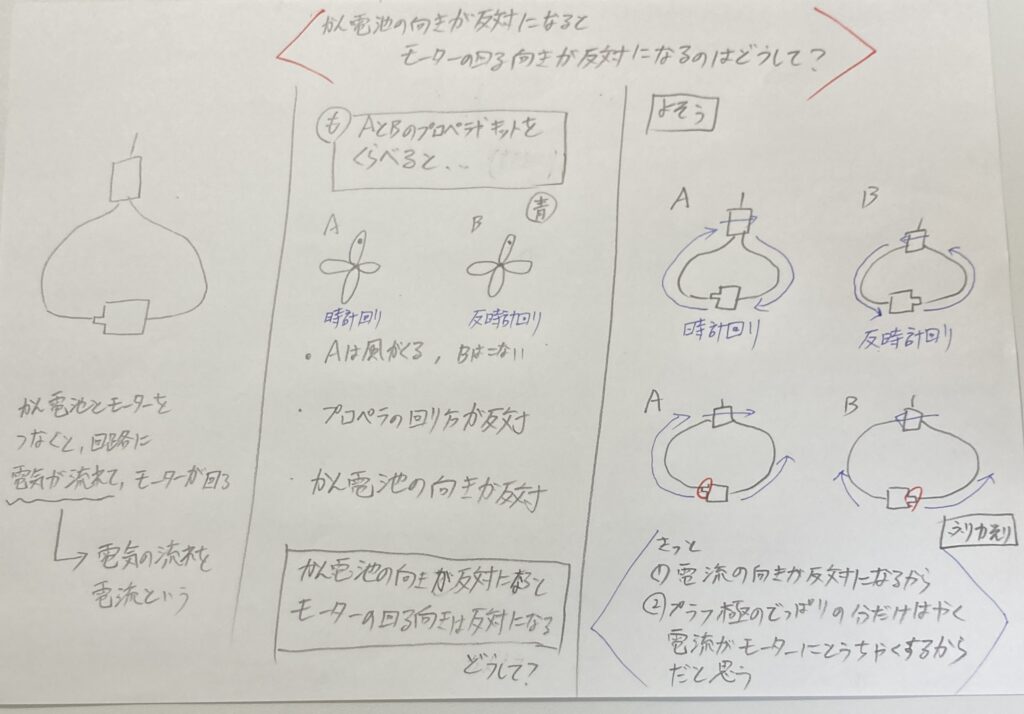
板書案

振り返りをする

C：前の学習の振り返りをしましょう

C：はい

C：Aさん

C：はい。前の学習の課題は、「モーターを回すにはどうすればいいのかな？」です

C：おなじです。はい

C：Bさん

C：はい。前の学習のまとめは、「乾電池をモーターにつなぐと回路に電気が流れてモーターが回ります」です

C：おなじです

T：そうだね。ほんで、回路に電気が流れるんだけど、この電気の流れのことを理科の言葉で・・・

C：電流

T：そうだね。ほんで、この単元のタイトルはなんだったんだっけ？

C：電流のはたらき

T：だったよね。つまり、電流がこの単元の主人公みたいなもんなんだよね。じゃあ、今日の勉強に入りましょう

問題を把握する

T：今日の問題を書きます

C：はい

C：かけました

T：そしたら、今回は２つのキットを準備しました。こんなふうにかごにいれてあるので、あとで班で１つもっていってください

C：はい

T：ほんで、この２つのプロペラやキットを比べてみて、気づいたことをノートにかいてください

C：わかりました

T：ほんで、１個気をつけてほしいことがあって、たとえばモーターを止めたり、動かしたりしたいときが来ると思います。その時は、青の導線を抜いたりつけたりするのはOKにします。色々いじっちゃうと準備している状態と違ってくるかもしれないからです

C：はい

T：なにか質問はありますか？

C：ないです

T：じゃあ、はじめてください

気づいたことを確認し、課題をつかむ

T：じゃあ、いったん手をとめてください

C：はい

T：気づいたことをおしえてください。

C：はい

T：Cさん

C：Aは風が当たるけど、Bは風が当たりませんでした

C：同じです。他にあります

C：Dさん

C：はい。プロペラの回り方が逆でした。

C：同じです

T：Aはどんなふうにまわっていた

C：こんな感じ

T：あ〜それのことを時計まわりっていいます。じゃあ、Bは？

C：反時計回り

T：すばらしい。本当にそうか、確認してみて

C：はい

C：やっぱりそうだ

T：なるほどね。他に気づいたことありますか？

C：はい

T：Eさん

C：AとBで乾電池の向きが反対になっていました

C：同じです

T：確認してみて

C：本当だ

T：じゃあ、これ乾電池の向き変えたらどうなるんだろうね？やってみて

C：あ〜反対になった

C：もどしたらまた、反対になった

T：つまり、乾電池の向きを反対にすると

C：プロペラの回る向きが反対になる

T：まあ、モーターの回る向きかな？プロペラはついているだけだから。じゃあ、かいておこう

T：じゃあ、きいていい？

C：はい

T：なんで、乾電池の向きを反対にすると、モーターの回る向きが反対になるんだろうね？

C：うーん

T：ということで、今日はこの不思議についてやっていきます。じゃあ、かだいどうする？

C：乾電池の向きが反対になると、モーターの回る向きが反対になるのはどうして？

T：じゃあ、それでいこう

ということで本時の課題として「乾電池の向きが反対になると、モーターの回る向きが反対になるのはどうして？」に決まりました。

予想をする

T：そしたら、予想をしてみましょう

C：はい

T：根拠のある予想にするときに大事なことは２つあります

C：日常生活とつなげる

C：習ったこととつなげる

T：そうだね。その２つのどちらかを意識して、予想を立ててみて

C：はい

T：そしたら、できた人は友達のやつ自由に見に行っておいで

C：はい

T：じゃあ、全員見に行っておいで。予想を立てれてない人もいいよ。ほんで、この人の予想なるほどなっていうのを選んでね

C：はい

C：できました

予想を交流する

T：だれのがよかった？

C：Fさん

C：Fさん

C：Gさん

T：じゃあ、Fさん多かった。Fさんおしえて

C：はい。私は、電流の向きが反対になるからだと思います。理由は、乾電池のプラス極、豆電球、乾電池のマイナス極っていうふうに習ったから、そんなふうに電流が流れていて、ほんで乾電池の向きを変えると電流も反対になると思ったからです

C：あ〜

C：？

T：グループでFさんは何を言いたかったのか相談

C：はい

C：できました

T：説明できる人？

C：はい

T：そしたら、Fさんにアドバイスね。言葉だけだとこれだけの人には伝わるの。でも、全員じゃないよね。これが１人でも増えるようにするにはどうすればいいと思う？

C：うーん

T：先生はね、図を使うことだと思う

T：そしたら、Fさんはここで学んでね。

T：じゃあ、図も使いながら、Fさんの考えを説明できる人いますか？

C：はい

T：Hさん

C：はい。電流の向きが反対になるからだと思います。理由は、乾電池のプラス極、豆電球、乾電池のマイナス極が１つのわのように・・・って習ったので、きっとプラス極から電流は流れているんだと思います。ほんで、Aの方はプラス極が左にあるので、こんなふうに電流が流れます

T：これ何回り？

C：時計回り

T：そうだね。続きどうぞ

C：はい。ほんで、Bの方はプラス極が右にあるので、反時計回りに回ります。そうすると電流の回り方が反対になるので、モーターも逆回りになるのではないかということだと思います

C：わかりました

T：わかったよ

C：はい

T：う〜ん。まだスッキリしない

C：はい

T：グループで相談

C：はい

C：できました

T：わかった？

C：はい

T：つまり、Fさんは何によってモーターの回る向きが決まると思っているの？
C：電流の向き

T：そうだね。ほんで、３年生の勉強で、「乾電池のプラス極、豆電球、乾電池のマイナス極が１つのわのように」っていう習ったことから、きっとプラス極から電流がでていて、乾電池を逆にすると、電流の向きが反対になるから、きっとモーターも反対になるってことだね

C：はい

T：Fさんいいよそうだね。Fさんは何とつなげたの？

C：習ったこと

T：そうだね。じゃあ、あとは、図を使えるとFさんはより多くの人にわかってもらえるってことだね

C：はい

T：がんばろう

C：はい！

T：あと、おもしろいなって思ったのは、Iさんかな。Iさんおしえて

C：はい。乾電池のプラス極ってボコンってなってるじゃないですか？そしたら、プラス極からもマイナス極からも電流は出ているんだけど、このボコンって出ている分だけ、はやくつくからAの方は、左から右に電流がながれます。でも、乾電池を逆にすると、今度は右側にプラス極がくるので、その分こっちがはやくつくからBの方は、右から左に電流が流れます

C：なるほど

T：Fさんとおなじですか？

C：ちがう

T：どこがちがうかをかくにんしながら、Iさんがどんな予想をしていたのか確認

C：はい

C：できました

T：まず、FさんとIさんはどこがちがった？

C：はい

T：Jさん

C：はい。Fさんは、プラス極から電流がでているから一方通行だけど、Iさんはプラス極からもマイナス極からも電流が出ているのが違うんだと思います

C：同じです

T：そうだね。ほんで、Iさんは、何の分だけはやくつくっていってた？

C：プラス極のボコンってなってるところ

T：ここだね。だから、その分早くつくから、電流の向きがかわるんじゃないんかだってさ

C：なるほど

根拠のある予想とは何かを説明し、まとめをする

T：でね、みんなの予想を見てて、磁石の勉強とかとつなげたり日常生活とつなげて考えたりしてた子もいるんだけど、今回は既習とつなげて考えてほしいなとおもってみてました。だって、タイトルはなに？

C：電流のはたらき

T：じゃあ、電流が絶対に関係するやん

C：たしかに

T：FさんとIさんのやつはどっちが正しいかはわからないけど、２人とも電流を根拠に予想を立てているよね。だから、どっちもそうかもしれんってならんかった？

C：なりました

T：これが根拠のある予想。なんでも繋げればいいってわけじゃなく、どういう予想をすればみんな納得するかなって視点で予想を立てれるといいな。まあ、まだ６月なので、３月に全員ができるようになりましょう

C：はい

T：ちなみに、２人の予想のどちらかが正解です

C：え〜

T：さあ、どっちが正解なんだろうね。じゃあ、まとめをするよ

C：はい

といって、本時のまとめとして、「きっと、①電流の向きが反対になるから、②プラス極のでっぱりの分だけはやく電流がモーターに到着するからだと思う」とかきました

T：じゃあ、ふりかえりをしましょう

C：はい

C：できました

T：じゃあ、次回は何をする？

C：実験方法を立てて、実験する

T：そうだね。じゃあ、おわりましょう

終わりに

　今回は、根拠のある予想とは何かについて授業を通して伝えました。「日常生活とつなげる」「既習とつなげる」って言葉では簡単だけど、その言葉の意味を実感させるのは難しいことです。そして、その力は授業でやりながらでしかつきません。

　自分で考える、良い見本を見る、いい予想の立て方のイメージをもつ、自分もやってみる、価値づけされる…このステップしかないと思います。だから、あせらず地道にコツコツと…です！