まだ９授業目を見ていない方は、先に理科専科がズバリ授業案を公開！ 〜５年「物のとけ方」９授業目〜をご覧ください。
＜本当に水の量を増やすと塩やミョウバンの溶ける量はふえるのか？＞
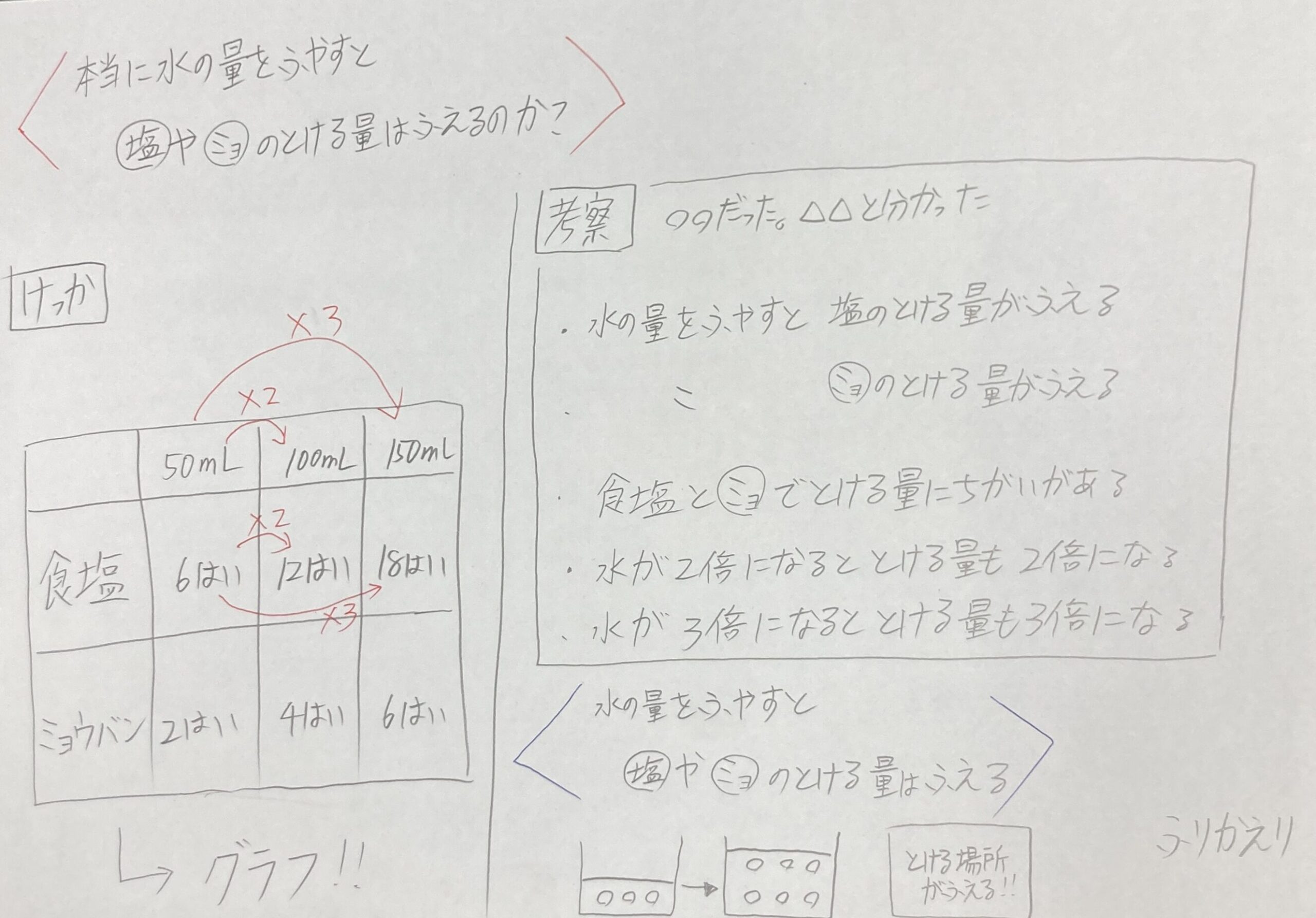
板書案
課題を読む
T：全員で課題を読みましょう。せーの
C：本当に水の量を増やすと塩やミョウバンの溶ける量はふえるのか？
T：ということで復習をします。前回は何をしたの？
C：実験をしました
T：そうだね。ほんでみんなの協力のお陰でこんな結果がわかったんだよね
C：はい
T：ちなみに、この結果をこんなふうにスプレッドシートに読み込ませると、こんなふうなグラフになりました。
C：お〜
T：じゃあ、今日は何をするの？
C：考察です。
T：そうだね。この結果をもとに考察をしていきましょうね
C：はい
考察を交流する
T：そしたら、考察の型は覚えている？
C：〇〇だった。このことから△△とわかった
T：そうだね。じゃあ、しばらく時間をあげるからかいてみて
C：はい
C：できました
T：じゃあ、どんな考察を書いたか教えて
C：はい
T：Aさん
C：しおは、５０ｍｌのときは６はい、１００ｍｌのときは１２はい、１５０mlのときは１８はいとけた。このことから水の量をふやすと、塩の溶ける量はふえるとわかった。
C：おなじです
C：他にあります。
C：Bさん
C：はい
C：ミョウバンは、５０ｍｌのときは２はい、１００ｍｌのときは４はい、１５０mlのときは６はいとけた。このことから水の量をふやすと、ミョウバンの溶ける量はふえるとわかった。
C：わかりました
C：他にあります。
C：Cさん
C：はい。しおは１５０ｍｌのとき１８はいで、ミョウバンは１５０ｍｌのとき６はいとけた。このことから食塩とミョウバンで溶ける量にちがいがあるとわかった
C：わかりました
C：他にあります。
C：Dさん
C：はい。しおは５０ｍｌのときは６はい、１００ｍｌのときは１２はい、１５０mlのときは１８はいとけた。このことから水の量が２ばいになると、溶ける量も２ばいになるし、水の量が３ばいになると、溶ける量も３ばいになるとわかりました
C：わかりました
T：どういうこと？
C：えっと、水の量が・・・
T：ちょっと先に友達と確認
C：できました
T：だれかこの表を使いながらおしえて
C：はい
T：Eさん
C：はい。水の量が５０ｍｌと１００ｍｌだと２倍になっていますよね。そしたら溶ける量も６と１２で２ばいになっています。それに５０ｍｌと１５０ｍｌだと３ばいになっていますよね。そしたら溶ける量も６と１８で３ばいになっています。
T：Dさんの言いたかったことあってる？
C：あってます
T：なるほどね。これを算数の言葉で
C：比例
T：そう。比例の関係といいます。つまり、２００ｍｌだったら、何杯とけそう？
C：２４はい
T：なんでそう言えるのかペアで相談
C：できました
T：おしえて
C：はい
T：Fさん
C：はい。５０ｍｌと２００ｍｌだと４倍になっていますよね。だから、６はいに４倍したら２４はいになるので２４はいとけるとおもいます
C：同じです
T：こういうきまりを見つけられるってすごいね
T：ほかに考察はありますか？
C：はい
T：Gさん
C：はい。ミョウバンは５０ｍｌのときは２はい、１００ｍｌのときは４はい、１５０mlのときは６はいとけた。このことから水の量が２ばいになると、溶ける量も２ばいになるし、水の量が３ばいになると、溶ける量も３ばいになるとわかりました
C：おなじです
T：なるほど。さっきは塩だったけど、今回は
C：ミョウバン
T：ミョウバンにもきまりがありそうだね
T：ほかにありますか？
C：ないです
まとめをし、ふりかえりをする
T：じゃあ、結局水を増やしたら溶ける量は増えるの？
C：ふえます
T：そうだね。
T：じゃあ、まとめはどうする？
C：水の量を増やしたら、塩やミョウバンの溶ける量は増える
T：じゃあ、それにしよう
ということで、本時のまとめとして、「水の量を増やしたら、塩やミョウバンの溶ける量は増える」に決まりました。
T：じゃあ、ふりかえりをしてね
C：はい
モデル図をかく
T：そしたら、モデル図を書こう
C：はい
T：まずビーカーと水をかきます。ほんで、粒を３つかきましょう
C：できました
T：溶ける量には限りがあるし、溶けたものは全体に同じように広がっているので、これ以上は溶けるスペースがないわけだね
T：でも、水がふえると・・・
C：溶けるスペースができる
T：そうだね。そうすると、またつぶが３つかけるね
C：はい
T：こんなふうに、水が２倍になると、溶けるスペースができて、それで溶ける量も２倍になるってわけだね
C：なるほど
終わりに
考察がどんどんかけるようになってきたのが今回の収穫だなと思いました。ある時まで、課題に対する考えを書くのが考察だよってしどうしていたのですが、「結果から言えること」というふうにゆるめたことで、多様な考察が出るようになりました。ただ、子どもたちには、課題に対する考えを書いたうえで、他にも言えることあれば書いてねというふうに指導をしています。理科の本質は、課題を解決することだからです。
続きが気になる方は、理科専科がズバリ授業案を公開！ 〜５年「物のとけ方」１１授業目〜をご覧ください。
コメント